读书笔记-《我的第一本算法书》
第一章:数据结构
链表
特性
- 呈线性排列的数据结构,元素中有字段指向下一个元素
内存
- 内存空间不连续
时间复杂度
-
删除:
-
直接在最后把指向被删除的元素改为指向被删除的下一个元素修改即可
-
时间复杂度:O(1)
-
-
添加:
-
直接在当前列表的最后的元素的指向另一个元素即可
-
时间复杂度:O(1)
-
-
查询:
-
需要从最开始的元素查询
-
时间复杂度:O(n)
-
扩展
- 循环链表,最后一个元素的下一个元素指向开头的元素
- 每个元素有两个指向,分别指向前一个元素和后一个元素
数组
特性
- 呈线性排列的数据结构,元素有下标
内存
- 元素在内存中是连续的
时间复杂度
-
添加:
-
首先需要在末尾增加需要的存储空间,把需要添加的位置以及以后的元素的下标全部+1,把需要添加的位置放进新的元素
-
时间复杂度:O(n)
-
-
删除:
-
依此把需要删除的位置的以后的元素的下标-1
-
时间复杂度:O(n)
-
-
查询:
-
根据下标直接随机访问
-
时间复杂度:O(1)
-
栈
特性
-
呈线性排列的数据结构;后进先出Last In First Out,简称 LIFO
-
push(入栈),pop(出栈)
时间复杂度
- 入栈和出栈,时间复杂度都是:O(1)
队列
特性
- 呈线性排列的数据结构;先进先出First In First Out,简称FIFO
- 入队,出队
时间复杂度
- 入队和出队的时间复杂度都是:O(1)
哈希表
特性
- 哈希表存储的是由键(key)和值(value)组 成的数据
- 如果在hash值不冲突时,哈希表的每个桶都只保存一个key;如果hash值冲突了,则会变成链表存储
- 先用key计算hash值,将得到的哈希值除以数组的长度,求得其余数、就找到了存储位置。这样的求余运算叫作“mod 运算”
- 如果两个key的hash值求余后找到的存储位置已经有值,这种存储位置重复了的情况便叫作“冲突”。遇到这种情况,可使用链表在已有数据的后面 继续存储新的数据
时间复杂度
- 哈希表的时间复杂度与hash算法有关
- 如果hash值不会冲突(理想情况),则新增、修改、删除、查询的时间复杂度都是:O(1)
- 如果hash值全部一致,则hash表其实就是一个链表,时间复杂度也与链表一致
补充说明
在存储数据的过程中,如果发生冲突,可以利用链表在已有数据的后面插入新数据 来解决冲突;这种方法被称为“链地址法”。
除了链地址法以外,还有几种解决冲突的方法。
其中,应用较为广泛的是“开放地址法”。这种方法是指当冲突发生时,立刻计算出一个候补地址(数组上的位置)并将数 据存进去。如果仍然有冲突,便继续计算下一个候补地址,直到有空地址为止。可以通过多次使用哈希函数或“线性探测法”等方法计算候补地址。
堆
特性
-
堆是一种图的树形结构,被用于实现“优先队列”(priority queues)。
-
优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺 序取出。
-
在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中。
-
堆中的节点最多有两个子节点,节点的排序为从上到下,同一行则从左到右。
-
堆中存储数据的规则:子节点必须大于父节点
时间复杂度
-
添加数据
- 增加节点时在最下面一行的最左边增加,如果最下面的一行没有位置则增加新的一行
- 如果增加的数据比父节点的数字小,则与父节点交换位置,重复此步骤直到比父节点大或者没有父节点为止
- 时间复杂度:O(logn)
-
取出数据
- 取出数据永远是取最上面节点的数据
- 最上面节点的数据被取走之后,需要重新调整
- 重新调整时,需要把最后的数据(即最下面一行最右边的节点)移动到最上面
- 然后与最上面的两个子节点做比较,如果数字小于两个子节点,则调整完成
- 如果最上面的数据大于子节点的数据,则与较小的子节点的位置进行交换,重复此操作直到所有父节点小于子节点为止
- 时间复杂度:O(logn)
二叉查找树
特性
-
二叉查找树(又叫作二叉搜索树或二叉排序树)是一种采用了图的树形结构的数据结构
-
每个节点最多有两个子节点
-
每个节点的值大于其左子树的任意节点的值
-
每个节点的值小于其右子树的任意节点的值
-
根据上面的特性,我们可以知道如果想要查找最小值,则在左边的最末端
时间复杂度
-
添加数据
- 从顶端开始查找添加位置
- 如果添加的值大于顶端的值,则往右移;小于它则往左移
- 时间复杂度:O(logn)
-
删除数据
- 如果删除的节点没有子节点,则直接删除此节点
- 如果删除的节点有一个子节点,则删除此节点后把子节点移到当前的节点
- 如果删除的节点有两个子节点,则删除此节点后把左边子节点的最右端移到当前节点(也可以把右边子节点的最左端移到当前节点)
- 上面的一句可以理解为:把小于被删除的节点的最大值移到删除的节点;或者把大于被删除节点的最小值移到删除节点
- 如果移动的节点还有子节点,也按照同样的方式移动
- 时间复杂度:O(logn)
-
查找数据
- 从顶端开始查找
- 如果大于查找节点的值,则向右移;如果小于查找节点的值,则向左移;循环此操作
- 时间复杂度:O(logn)
扩展
关于时间复杂度
- 如果数的形状比较均衡,查找的时间复杂度是O(logn)
- 如果不均衡极端情况下是一个链表,查找的时间复杂度是O(n)
以二叉查找树为基础扩展的数据结构
- “平衡二叉查找树”:这种数据结构可以修正形状不均衡的树,让其始终保持均衡形态,以提高查找效率
- “B 树”:二叉查找树中一个结点最多有两个子结点,如果我们把子结点数扩展为 m(m 为预先设定好的常数)。像这种子结点数可以自由设定,并且形状均衡的树便是 B 树
第二章:排序
冒泡排序
算法释义
冒泡排序就是重复“从序列右边开始比较相邻两个数字的大小,再根据结果交换两个数字 的位置”这一操作的算法。
在这个过程中,数字会像泡泡一样,慢慢从右往左“浮”到序列的 顶端,所以这个算法才被称为“冒泡排序”。
时间复杂度:O(n²)
在冒泡排序中:
-
第 1 轮需要比较 n -1 次
-
第 2 轮需要比较 n -2 次
-
第 n -1 轮需 要比较 1 次
因此,总的比较次数为 (n -1) +(n -2) +…+1 ≈ n² /2。这个比较次数恒定为 该数值,和输入数据的排列顺序无关。
Java代码实现
选择排序
算法释义
- 选择排序就是重复“从待排序的数据中寻找最小值,将其与序列最左边的数字进行交换” 这一操作的算法。
- 在序列中寻找最小值时使用的是线性查找。
时间复杂度:O(n²)
选择排序使用了线性查找来寻找最小值,因此在
- 第 1 轮中需要比较 n - 1 个数字
- 第 2 轮需要比较 n - 2 个数字
- 到第 n - 1 轮的时候就只需比较 1 个数字
- 因此,总的比较次数与冒泡排序的相同,都是(n-1)+(n-2)+…+1 ≈ n2/2 次。
Java代码实现
插入排序
算法释义
插入排序是一种从序列左端开始依次对数据进行排序的算法。
在排序过程中,左侧的数据陆续归位,而右侧留下的就是还未被排序的数据。
插入排序的思路就是从右侧的未排序区域内取出一个数据,然后将它插入到已排序区域内合适的位置上。
时间复杂度:O(n²)
Java代码实现
堆排序
算法释义
堆排序的特点是利用了数据结构中的堆
- 首先,在堆中存储所有的数据,并按降序来构建堆
- 然后从堆中取出数据,并把取出的数据放在最右边的空位置
时间复杂度:O(nlogn)
堆排序一开始需要将 n 个数据存进堆里,所需时间为 O(nlogn)
每轮取出最大的数据并重构堆所需要的时间为 O(logn)
由于总共有 n 轮,所以重构后排序的时间也是 O(nlogn)
因此,整体来看堆排序的时间复杂度为 O(nlogn)
Java代码实现
暂无
归并排序
算法释义
归并排序算法会把序列分成长度相同的两个子序列,当无法继续往下分时(也就是每个子序列中只有一个数据时),就对子序列进行归并。
归并指的是把两个排好序的子序列合并成一个有序序列。
该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
时间复杂度:O(nlogn)
- 把数组拆分成不可分割的最小单元的数组,时间复杂度O(n)
- 依次把所有数组进行合并排序,每一轮的比较次数为O(n);需要进行logn轮
- 最终的时间复杂度是O(nlogn)
Java代码实现
快速排序
算法释义
-
快速排序算法首先会在序列中随机选择一个基准值(pivot)
-
然后将除了基准值以外的数分为“比基准值小的数”和“比基准值大的数”这两个类别,再将其排列成以下形式。
- [ 比基准值小的数 ] 基准值 [ 比基准值大的数 ]
-
接着,对两个“[ ]”中的数据进行排序之后,整体的排序便完成了。对“[ ]”里面的数据进行排序时同样也会使用快速排序。
时间复杂度:O(nlogn)
- 每一轮比较的次数为n次,时间复杂度O(n)
- 需要进行logn轮的比较
- 最终的时间复杂度是O(nlogn)
Java代码实现
扩展
基准值约接近数组的平均值,排序的速度越快;基准值一般都使用第一个数字
第三章:数组的查找
线性查找
特性
- 遍历整个数组,逐个进行比较,直到找到为止
时间复杂度:O(n)
Java代码实现
二分查找
特性
- 只能查找已经排好序的数组
- 每次查找取中间位置的值与需要查找的数字比较,如果中间值大于待查找数据,则继续在中间值左边的数组进行查找;反之亦然
时间复杂度 O(logn)
- 每一次查找都会把待查找的范围缩小一半,直到结束为止
- 查找需要logn轮,每一轮比较1次;所以时间复杂度为O(logn)
Java代码实现
第四章:图的搜索
图的定义
计算机科学或离散数学中说的“图”是下面这样的:
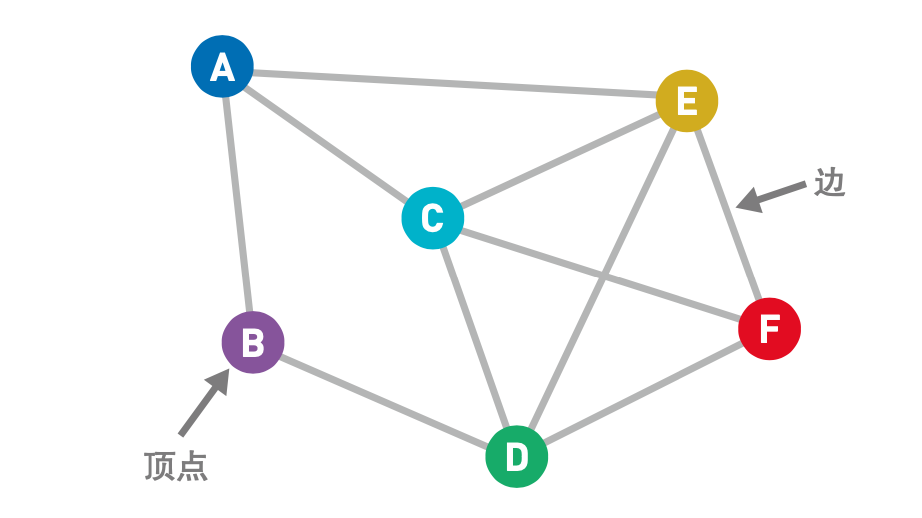
上图中的圆圈叫作“顶点”(也叫“结点”),连接顶点的线叫作“边”。也就是说,由顶点和连接每对顶点的边所构成的图形就是图。图可以表示各种关系
加权图
我们可以给边加上一个值,这个值叫作边的“权重”或者“权”,加了权的图被称为“加权图”。
没有权的边只能表示两个 顶点的连接状态,而有权的边就可以表示顶点之间的“连接程度”。
所谓“程度”在不同的场景意思也不一样:
- 地铁线路图两站之间的权是两站之间的距离
- 同样是地铁线路图,两站之前的权也可以是两站之间的时间
- 如果是高铁站线路图,两站之间的权也可以表示两站之间的乘车费
有向图
当我们想在路线图中表示该路线只能单向行驶时,就可以给边加上箭头,而这样的图就叫 作“有向图”。
和无向图一样,有向图也可以在边上添加权重,而且根据方向的不同,权重也不一样。
如下图中,如果权重表示花费时间,则B点到C点是下坡路,反过来C到B就是上坡路。
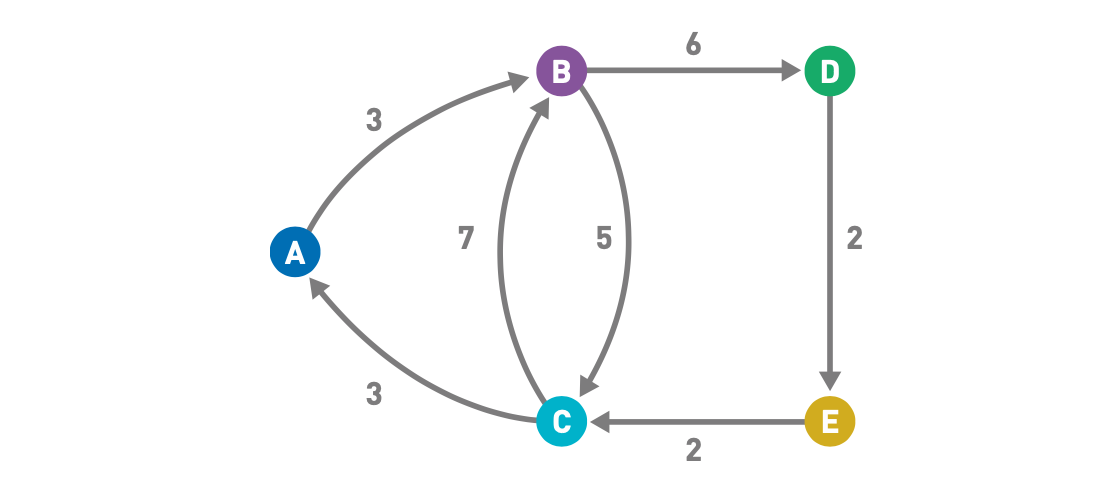
图能给我们带来哪些便利
假设图中有两个顶点 s 和 t,而我们设计出了一种算法, 可以找到“从 s 到 t 的权重之和最小”的那条路径,如:
- 寻找计算机网络中通信时间最短的路径
- 寻找路线图中耗时最短的路径
- 寻找路线图中最省乘车费的路径
图在代码中如何实现
- 图是用来表示节点与节点的关系的,所以可以使用Map来实现图
- 有向图,如上面图两个节点A和B、map中key为A的值有B,而key为B的值没有A,就可以表示方向
- 加权图,同样适用Map实现,区别是在value中既包含下一个节点的信息,又包含权重信息加权图Java实现
图的搜索
广度优先搜索
假设我们一开始位于某个顶点(即起点),此时并不知道图的整体结构,而我们的目的是从起点开始顺着边搜索,直到到达指定顶点(即终点)。
在此过程中每走到一个顶点,就会判断一次它是否为终点。广度优先搜索会优先从离起点近的顶点开始搜索。
Java代码实现
深度优先搜索
深度优先搜索会沿着一条路径不断往下搜索直到不能再继续为止,然后再折返,开始搜索下一条候补路径。
Java代码实现
广度优先搜索和深度优先搜索对比
广度优先搜索选择的是最早成为候补的顶点,因为顶点离起点越近就越早成为候补,所以会从离起点近的地方开始按顺序搜索;
而深度优先搜索选择的则是最新成为候补的顶点,所以会一路往下,沿着新发现的路径不断深入搜索。
贝尔曼 - 福特算法
解决的问题
-
贝尔曼 - 福特(Bellman-Ford)算法是一种在图中求解最短路径问题的算法。
-
最短路径问题就是在加权图指定了起点和终点的前提下,寻找从起点到终点的路径中权重总和最小的那条路径。
求解的步骤
- 首先设置各个顶点的初始权重 :起点为 0,其他顶点为无穷大(∞);这个权重的意思是从起点到当前节点的最短路径暂定值。
- 从起点(A)开始遍历,找到子节点(B),更新子节点的权重:min(A的权重+A到B边的权重,B节点权重)
- 循环上面的步骤一直更新所有节点
时间复杂度O(nm)
- 将图的顶点数设为 n、边数设为 m。
- 该算法经过 n 轮更新操作后就会停止,而在每轮更新操作中都需要对各个边进行 1 次确认
- 因此 1 轮更新所花费的时间就是 O(m),整体的时间复杂度就是 O(nm)
Java代码实现
狄克斯特拉算法
解决的问题
狄克斯特拉(Dijkstra)算法也是求解最短路径问题 的算法,使用它可以求得从起点到终点的路径中权重总和最小的那条路径。
求解的步骤
- 首先设置各个顶点的初始权重 :起点为 0,其他顶点为无穷大(∞);这个权重的意思是从起点到当前节点的最短路径暂定值。
- 从起点出发,寻找可以从目前所在的顶点直达且尚未被搜索过的顶点。
- 计算各个候补顶点的权重。计算方法是“目前所在顶点的权重+目前所在顶点到候补顶点的权重”。
- 如果计算结果小于候补顶点的值,就更新这个值。
- 从候补顶点中选出权重最小的顶点,作为下一个被搜索的点,这一点与贝尔曼-福特算法不一样
时间复杂度
将图的顶点数设为 n、边数设为 m,那么如果事先不进行任何处理,该算法的时 间复杂度就是 O(n2)。
不过,如果对数据结构进行优化,那么时间复杂度就会变为 O(m + nlogn)。
Java代码实现
贝尔曼福特算法和迪克斯特拉算法对比
说明
如果在一个闭环中边的权重总和是负数,那么只要不断遍历这个闭环,路径的权重就能不断减小,也就是说根本不存在最短路径。
贝尔曼 - 福特算法可以直接认定不存在最短路径,但在狄克斯特拉算法中,即便不存在最短路径,它也会 算出一个错误的最短路径出来。因此,有负数权重时不能使用狄克斯特拉算法。
总的来说,就是不存在负数权重时,更适合使用效率较高的狄克斯特拉算法,而存 在负数权重时,即便较为耗时,也应该使用可以得到正确答案的贝尔曼 - 福特算法。
A*(A-Star)算法
解决的问题
A-Start算法也是解决在图中求解最短路径问题的算法,由狄克斯特拉算法发展而来。
狄克斯特拉算法会从离起点近的顶点开始,按顺序求出起点到各个顶点的最短路径。
也就是说,一些离终点较远的顶点的最短路径也会被计算出来,但这部分其实是无用的。
与之不同,A* 就 会预先估算一个值,并利用这个值来省去一些无用的计算
第五章 安全算法
安全和算法
传输数据时的四个问题
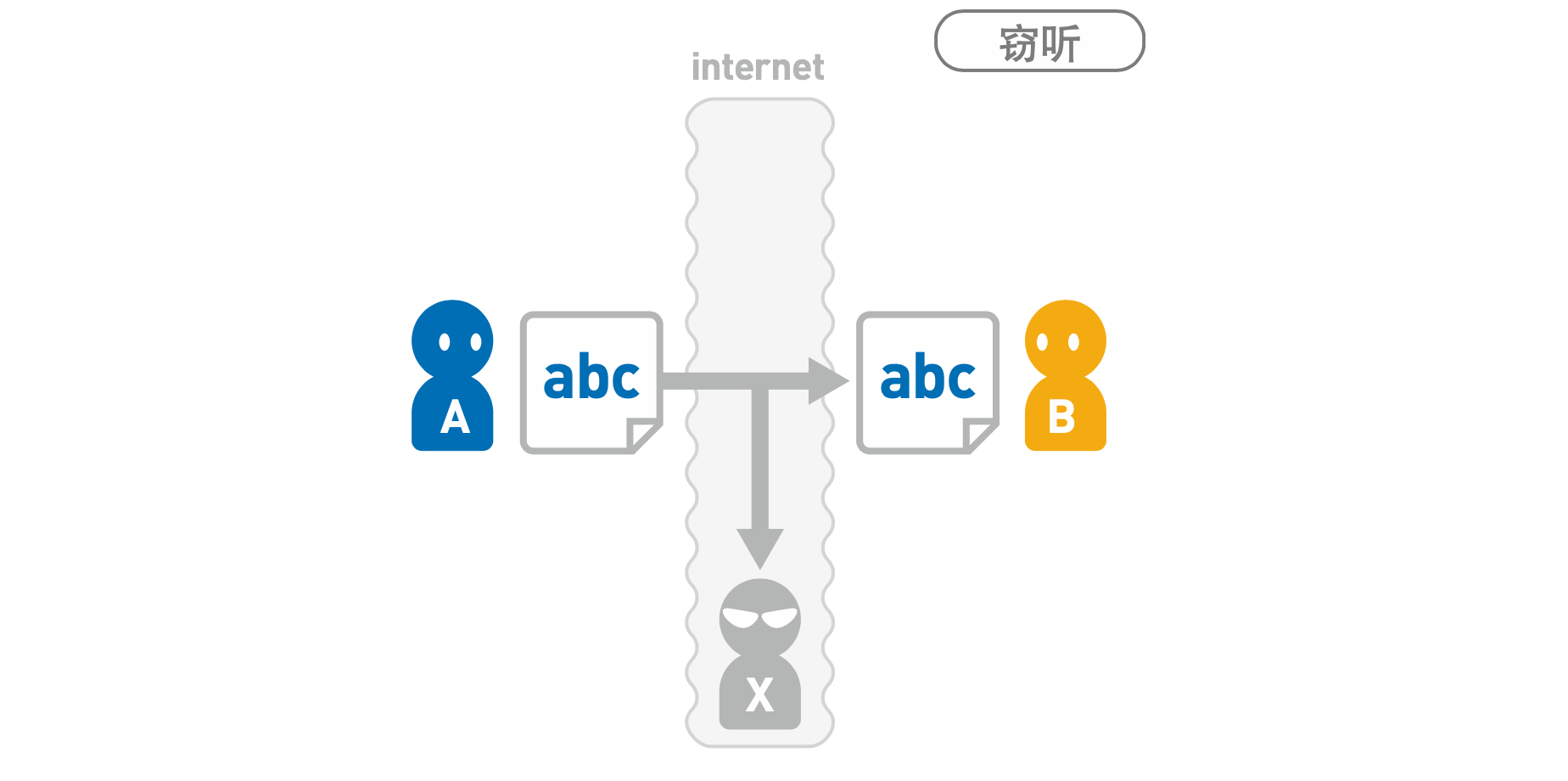
窃听
A 向 B 发送的消息可能会在传输途中被 X 偷看(如下图)。这就是“窃听”。
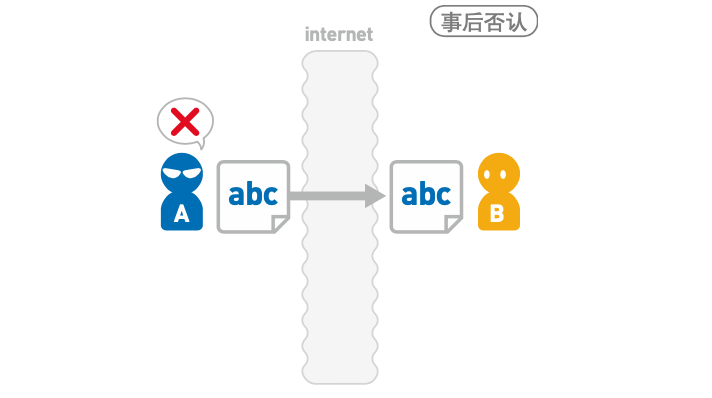
假冒
A 以为向 B 发送了消息,然而 B 有可能是 X 冒充的(如下图);反过来,B 以为从 A 那里收到了消息,然而 A 也有可能是 X 冒充的。
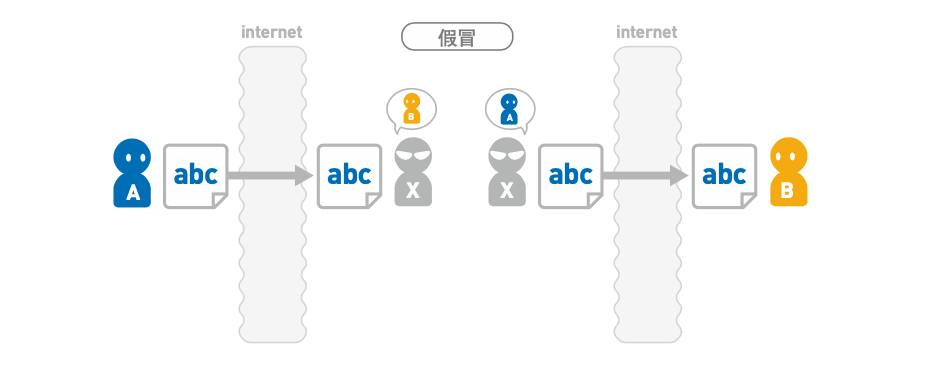
篡改
即便 B 确实收到了 A 发送的消息,但也有可能像右图 这样,该消息的内容在途中就被 X 更改了。
除了被第三者篡改外,通 信故障导致的数据损坏也可能会使消息内容发生变化。
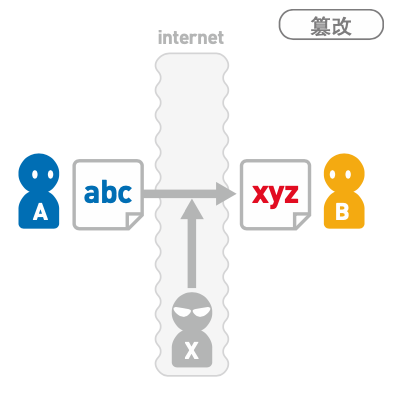
事后否认
B 从 A 那里收到了消息,但作为消息发送者的 A 可 能对 B 抱有恶意,并在事后声称“这不是我发送的消息”。
解决这些问题的安全技术
-
为了应对“窃听”,我们会使用“加密” 技术。
-
为了应对“假冒”,我们会使用“消息认证码”(下图左)或“数字签名”(下图右)技术。
-
为了应对“篡改”,我们同样会使用 “消息认证码”或“数字签名”技术。
-
其中“数字签名”技术还可以用于预防“事后否认”。
哈希函数
-
哈希函数可以把给定的数据转换成固定长度的无规律数值。
-
转换后的无规律数值可以作为数据摘要应用于各种各样的场景。
希函数的特征:
- 第一个特征是输出的哈希值数据长度不变。(不论输入的参数长短,得到的哈希值是定长的)
- 第二个特征是如果输入的数据相同,那么输出 的哈希值也必定相同。
- 第三个特征是即使输入的数据相似,但哪怕它们只有一比特的差别,那么输出的哈希值也会有很大的差异。
- 第四个特征是即使输入的两个数据完全不同,输 出的哈希值也有可能是相同的;这种情况叫作“哈希冲突”。
- 第五个特征是不可能从哈希值反向推算出原本的数据。(输入和输出不可逆)
哈希函数的算法中具有代表性的是 MD5 1、SHA-1 2和 SHA-2 等。其中 SHA-2 是现 在应用较为广泛的一个,而 MD5 和 SHA-1 存在安全隐患,不推荐使用。
应用示例
将用户输入的密码保存到服务器时也需要用到哈希函数。
如果把密码直接保存到服务器,可能会被第三者窃听,因此需要算出密码的哈希值,并只存储哈希值。
当用户输入密码时,先算出该输入密码的哈希值,再把它和服务 器中的哈希值进行比对。
共享密钥加密(对称加密)
共享密钥加密是加密和解密都使用相同密钥的一种加密方式。
实现共享密钥加密的算法有凯撒密码、AES 1、DES 2、动态口令等,其中 AES 的应用最 为广泛。
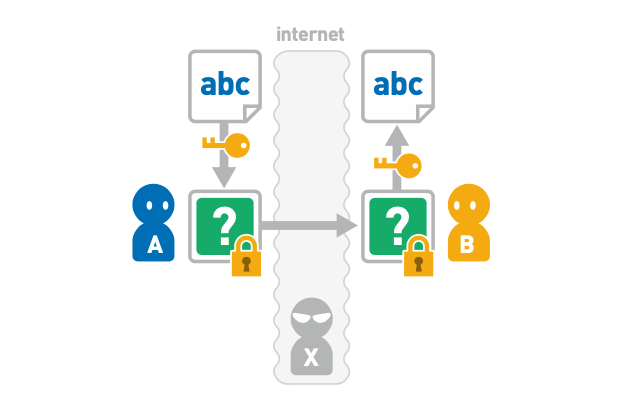
存在密钥分配问题
如上图,如果在A给B发送密钥时,被X监听了,则X就能用相同的密钥解密截获的密文。
公开密钥加密(非对称加密)
-
公开密钥加密是加密和解密使用不同密钥的一种加密方法。
-
由于使用的密钥不同,所以这种算法也被称为“非对称加密”。
-
加密用的密钥叫作“公开密钥”,解密用的叫作“私有密钥”。
实现公开密钥加密的算法有 RAS 算法、椭圆曲线加密算法等,其中使用最为广泛的是 RSA 算法。
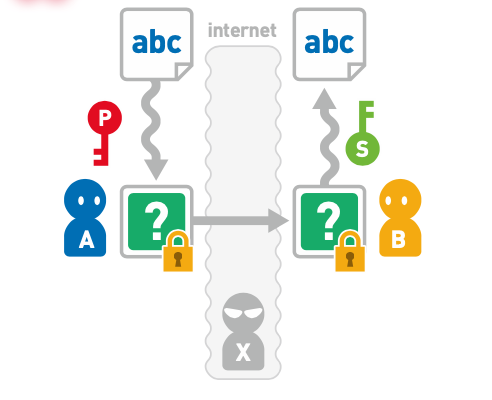
不存在密钥分配问题
公开密钥和密文都是通过互联网传输的,因此可能会被 X 窃听。
但是,使用公开密钥无法解密密文,因此 X 也无法得到原本的数据。
密钥数量不会过多
只需要生成一对公私钥,就可以把公钥共享给n个人使用。
对称加密就的密钥数量会随着人的增多而增多。
公开密钥加密存在公开密钥可靠性的问题
如下图,加入B在把公钥Pb共享给A的时候,被X截获了;X把自己的公钥Px发送给了A。
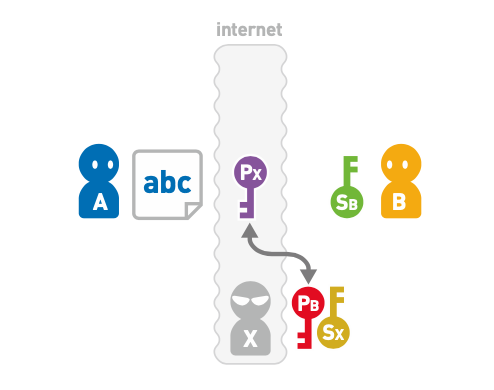
这时A在不知情的情况下使用Px对数据进行加密发送给B时,X截获密文就可以通过私钥Sx进行解密。
然后X可以截获的通过公钥Pb加密恶意数据发送给B,B能够使用自己的密钥Sb进行解密,以为数据是A发送的。
如下图所示:
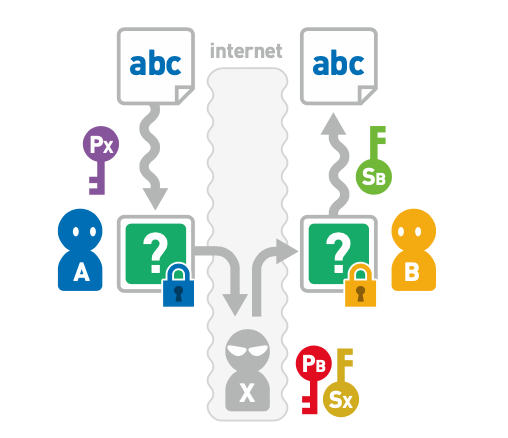
非对称加密算法的条件
- 可以使用某个数值对数据进行加密(计算)。
- 使用另一个数值对加密数据进行计算就可以让数据恢复原样。
- 无法从一种密钥推算出另一种密钥。
混合加密
共享密钥加密存在无法安全传输密钥的密钥分配问题,公开密钥加密又存在加密解密速度较慢的问题。
在混合加密中,要用处理速度较快的共享密钥加密对数据进行加密。不过,加密时使用的密钥,则需要用没有密钥分配问题的公开密钥加密进行处理。混合加密可以拆分成下面两步操作:
1、A在给B发送数据之前,先使用非对称的公钥对”对称加密的密钥“进行加密,然后把加密后的密文发送给A,A解密后就得到了”对称加密的密钥“。如下图:
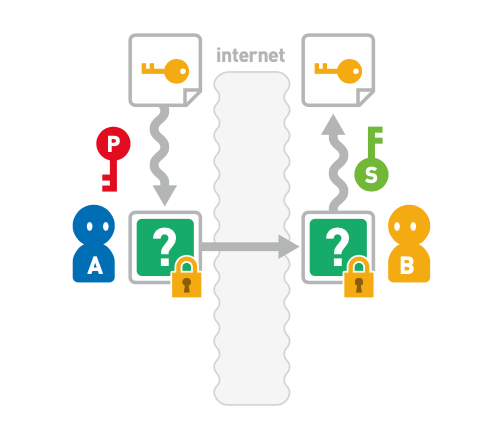
2、发送数据时,A使用”对称加密的密钥“对数据进行加密,然后发送给B,这样B就能使用之前收到的”对称加密的密钥“对数据进行解密。如下图:
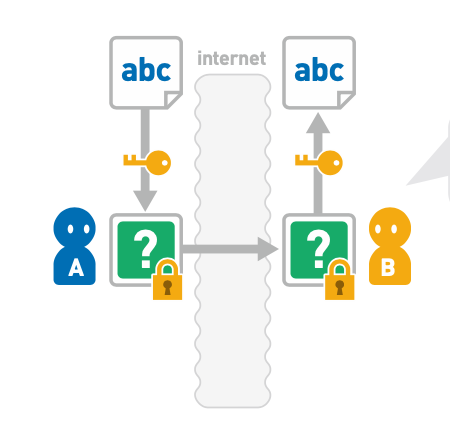
迪菲 - 赫尔曼密钥交换
迪菲 - 赫尔曼(Diffie-Hellman)密钥交换是一种可以在通信双方之间安全交换密钥的方法。
这种方法通过将双方共有的秘密数值隐藏在公开数值相关的运算中,来实现双方之间密钥的安全交换。
算法的概念
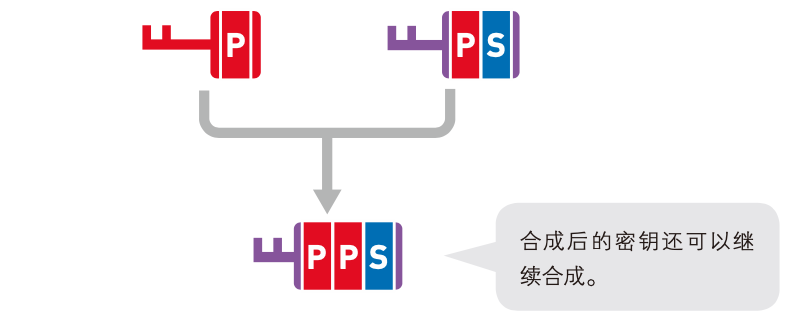
假设有一种方法可以合成两个密钥。使用这种方法来合成密钥P和密钥S,就会得到由这两个密钥的成分所构成的密钥 P-S。
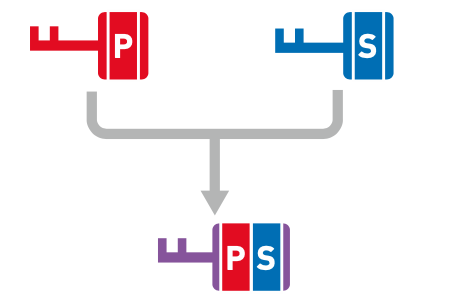
这种合成方法有三个特征。
- 第一,即使持有密钥 P 和合成的密钥 P-S,也无法把密钥 S 单独取出来。
- 第二,不管是怎样合成而来的密钥,都可以把它作为新的元素,继续与别的密钥进行合成。如下图,使用密钥 P 和密钥 P-S,还能合成出新的密钥 P-P-S。
- 第三,密钥的合成结果与合成顺序无关,只与用了哪些密钥有关。比如合成密钥 B 和密钥 C 后,得到的是密 钥 B-C,再将其与密钥 A 合成,得到的就是密钥 A-B-C。而合成密钥 A 和密钥 C 后,得到的是密钥 A-C, 再将其与密钥 B 合成,得到的就是密钥 B-A-C。此处的密钥 A-B-C 和密钥 B-A-C 是一样的。
密钥的交换
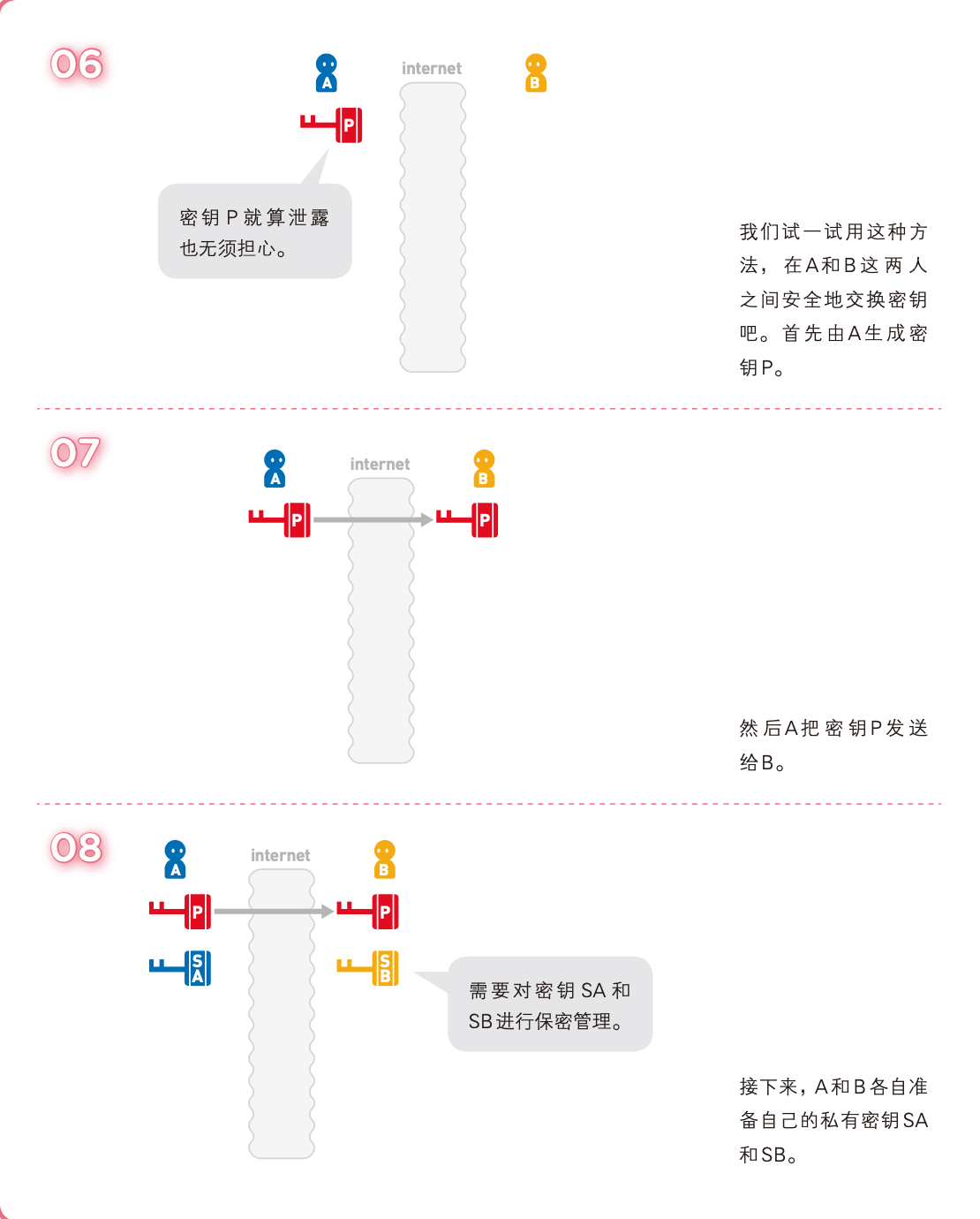
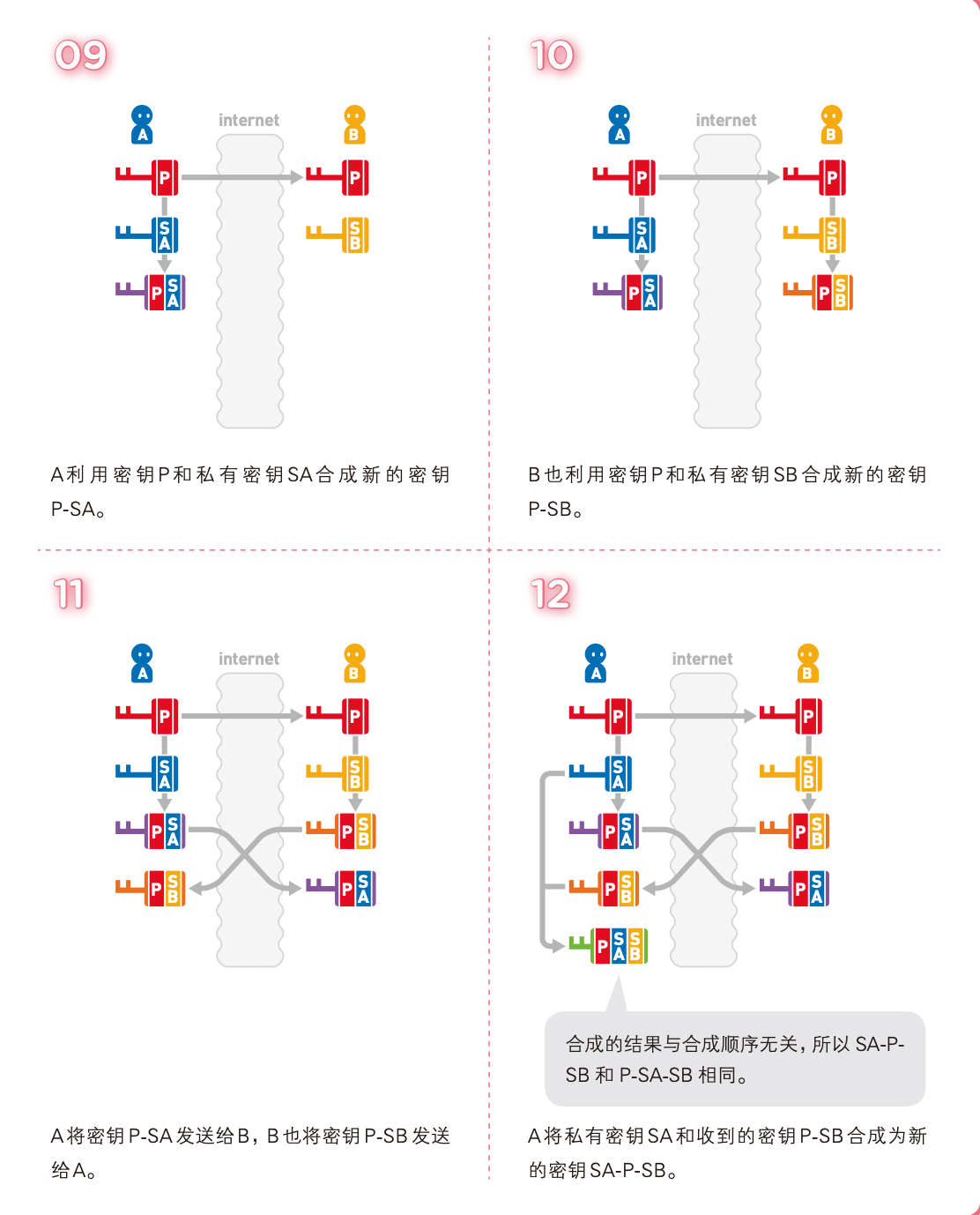
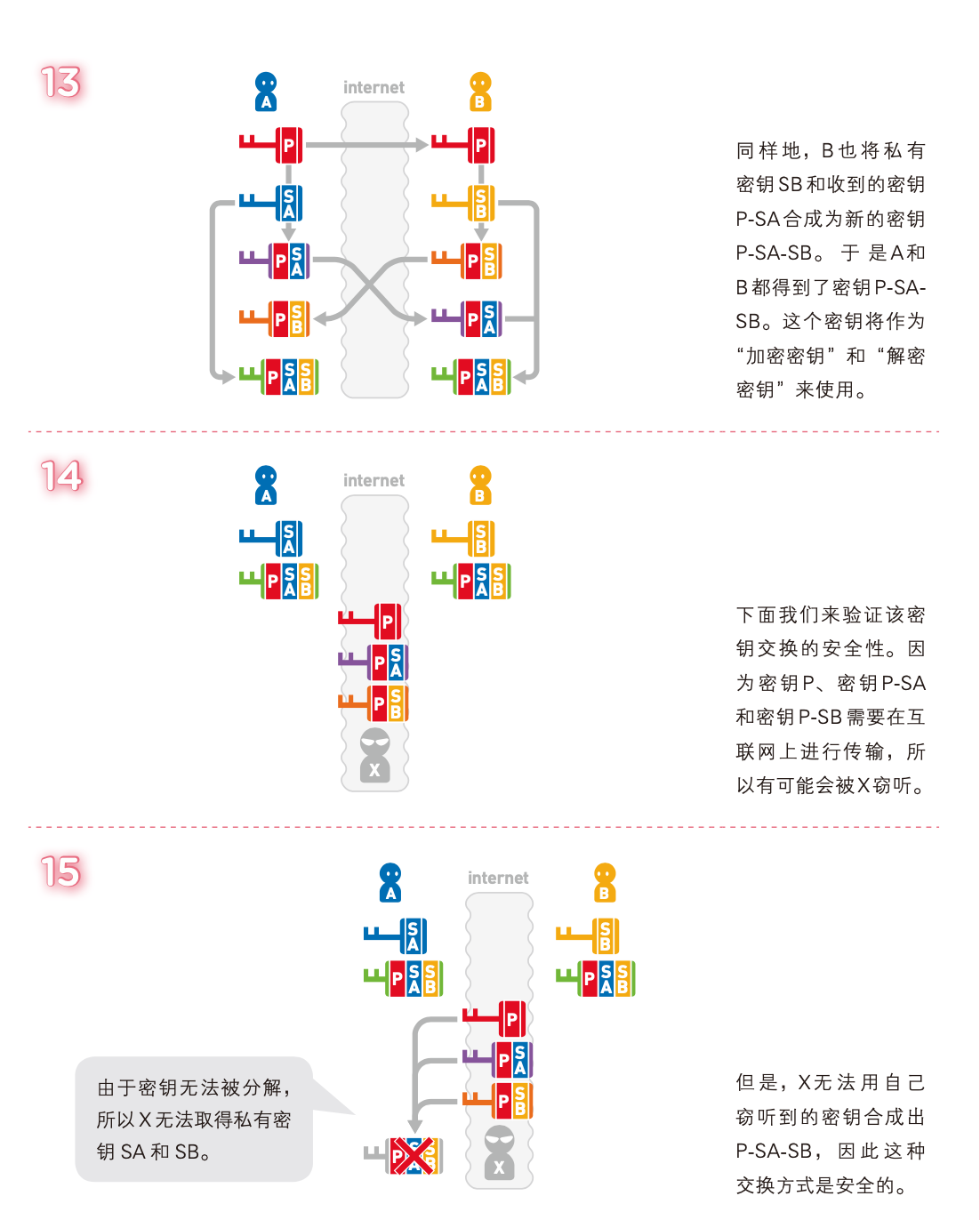
消息认证码,MAC(Message Authentication Code)
消息认证码可以实现“认证”和“检测篡改”这两个功能。
举个例子,如下图,假设 A 发送给 B 的密文(abc)在通信过程中被 X 恶意篡改了,而 B 收到密文后没有意识到这个问题。
B对密文进行解密可能无法解密或者解密后的数据是xyz。如果A在向B进行商品订购,如果B解密出的密文是xyz,就会给A发送xyz商品从而导致问题。
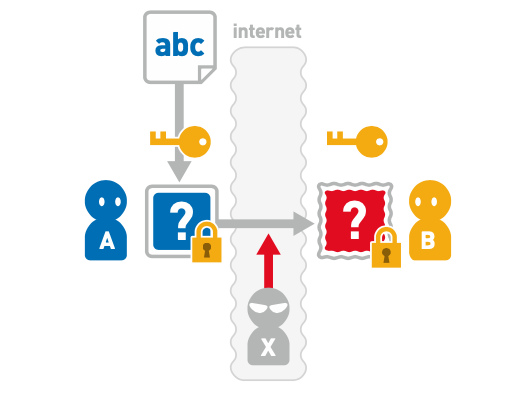
如何使用消息认证码解决篡改问题呢?
- A在发送数据之前,先生成一个用于制作消息验证码的密钥(key),然后用安全的方法(如混合加密)发送给B
- A对数据进行加密,并且使用第一步生成的key和密文生成一个数值,此值就是MAC
- A把MAC和密文一起发送给B
- B接收到密文和MAC后,先使用第一步A发送过来的key和密文使用同样的方法生成一个数值;并且使用此数值和收到的MAC进行比对
- 如果比对一致,则说明数据未被篡改
- 如果比对不一致,则说明数据被篡改了,直接丢弃数据;然后通知A重发
如果MAC和密文都被X截获了怎么办?
- X可以修改密文,此时B使用被篡改后的密文和key生成的数值不等于MAC,就能确认通信过程中发生了篡改
- X如果篡改了MAC,也与上一步一样,B也能确认通信过程中发生了篡改
- X既篡改了密文也篡改了MAC,因为X没有生成MAC的key,所以B收到被篡改后的数据时同样能确认发生了篡改
我们可以把 MAC 想象成是由密钥和密文组成的字符串的“哈希值”。
计算 MAC 的算法有 HMAC 1、OMAC 2、CMAC 3等。目前,HMAC 的应用最为广泛。
消息验证码无法防止“事后否认”
然而,这种方法也有缺点。在使用消息认证码的过程中,AB 双方都可以对消息进行加密并且算出 MAC。
也就是说,我们无法证明原本的消息是 A 生成的还是 B 生成的。 因此,假如 A 是坏人,他就可以在自己发出消息后声称“这条消息是 B 捏造的”,而否认自己的行为。如果 B 是坏人,他也可以自己准备一条消息,然后声称“这是 A 发 给我的消息”。
数字签名
数字签名不仅可以实现消息认证码的认证和检测篡改功能,还可以预防事后否认问题的发生。
由于在消息认证码中使用的是共享密钥加密,所以持有密钥的收信人也有可能是消息的发 送者,这样是无法预防事后否认行为的。
而数字签名是只有发信人才能生成的,因此使用它就可以确定谁是消息的发送者了。
数字签名的特征
比如A给B发送消息,那么数字签名必须满足下面两个条件:
- 只要发送的消息上有 A 的数字签名,就能确定消息的发送者就是 A。
- B 可以验证数字签名的正确性,但无法生成数字签名。
如何实现数字签名
先回想一下非对称加密的流程,A给B发送消息时使用B提供的公钥进行加密,B使用自己的私钥进行解密。如下图:
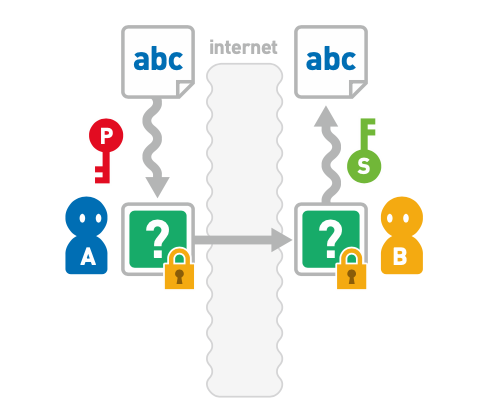
那么我们把这个过程反过来,就可以做到数字签名,如下图:
- A 使用自己的私有密钥加密消息。加密后的消息就是数字签名。
- A把数字签名和原始的数据都发送给B
- B接收到数字签名和数据后,使用A提供的公钥进行解密,并把解密后的数据和发送来的数据做比对
- 如果一致,则说明此消息是由A发送的,因为A的公钥只能解密经有A的私钥加密的数据
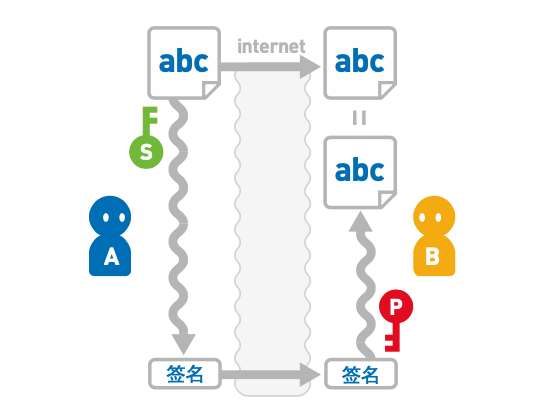
能够用 A 的公开密钥解密的密文,必定是由 A 生成的。因此,我们可以利用这个结论来确认消息的发送者是否为 A,消息是否被人篡改。
由于 B 只有公开密钥,无法生成 A 的签名,所以也预防了“事后否认”这一问题的 发生。
在使用此方式进行加密时,A使用自己的私钥加密的数据最好没有任何意义,只是用来验证发送着是否是A,并且没有被篡改。
数字证书
“公开密钥加密”和“数字签名”无法保证公开密钥确实来自信息的发送者。因此,就算公 开密钥被第三者恶意替换,接收方也不会注意到。
而数字证书,就能保证公开密钥的正确性。
如何使用数据证书发送公钥
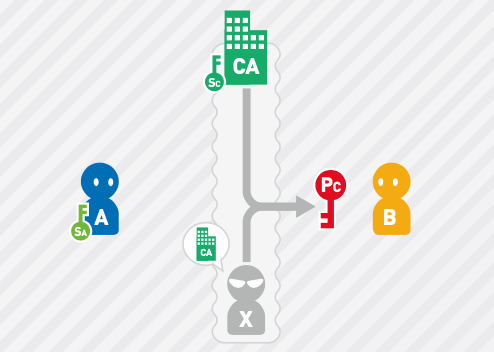
A持有公开密钥Pa 和 A私有密钥 Sa ,现在想要将公开密钥PA发送给B,如何做呢?
- A首先需要向认证中心 (Certification Authority, CA)申请发行证书,证明公开密钥PA 确实由自己生成
- 认证中心里保管着他们自己准备的公开密钥Pc和私有密钥 Sc
- A将公开密钥Pa 和包含邮箱信息的个人资料发送给认证中心
- 认证中心对收到的资料进行确认,判断其是否为A本人的资料。确认完毕后,认证中心使用自己的私有密钥 Sc,根据 A 的资料生成数字签名。
- 认证中心将生成的数字签名和资料放进同一个文件中,并把这个文件发送给 A。(这个文件就是 A 的数字证书)
- A 将作为公开密钥的数字证书发送给了 B。
- B 收到数字证书后,确认证书里的邮件地址确实是 A 的地址。接着,B 获取了认证中心的公开密钥。
- B 对证书内的签名进行验证,判断它是否为认证中心给出的签名。证书中的签名只能用认证中心的公开密钥 Pc 进行验证。如果验证结果没有异常,就能说明这份证书的确由认证中心发行。
- 确认了证书是由认证中心发行的,且邮件地址就是 A的之后,B从证书中取出A的公开密钥PA。这样,公开密钥便从 A 传到 了B。
经过以上步骤信息的接收者B可以确认公开密钥的制作者是A。
循环质疑,我们从认证中心获取的公钥Pc真的来自认证中心吗
由于公开密钥自身不能表示其制作者,所以有可能是冒充认证中心的 X 所生成的。也就是说,这里同样存在公开密钥问题(请参考下图)。
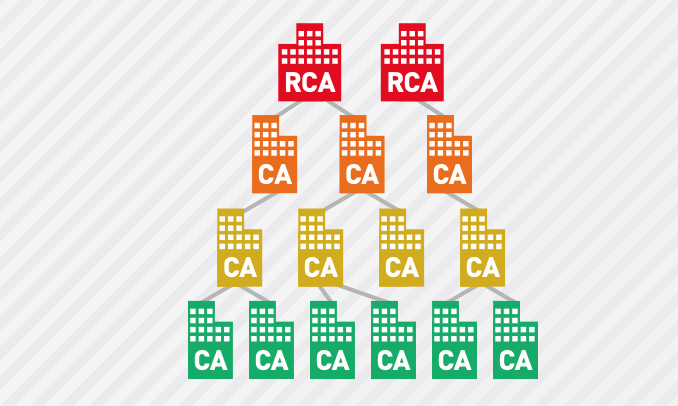
实际上,认证中心的公开密钥 PC 是以数字证书的形式交付的,会有更高级别的认证 中心对这个认证中心署名(请参考下图)。
所以我们有所怀疑可以一直验证下去。
最顶端的认证中心被称为“根认证中心”(root CA),其自身的正当性由自己证明。
第六章 聚类
什么是聚类
将相似的对象分为一组
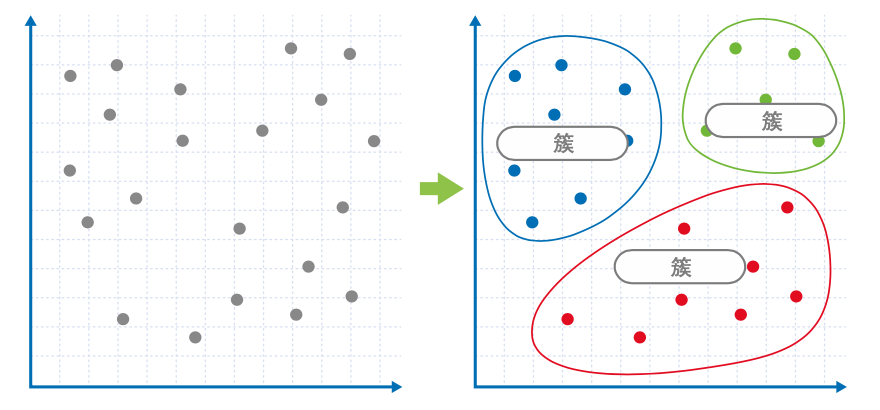
聚类就是在输入为多个数据时,将“相似”的数据分为一组的操作。1个组就叫作1个 “簇”。
下面的示例中每个点都代表 1 个数据,在平面上位置较为相近、被圈起来的点就代表一类相似的数据。
也就是说,这些数据被分为了 3 个簇。
如何定义“相似”
定义数据间的差距
根据数据类型不同,定义该数据是否“相似”的标准也不同。具体来说,就是要对两个数 据之间的“差距”进行定义。
如:假设某所高中的某个年级中共有 400 名学生,现在我们想要将这些学生在考试中取得的语 文、数学、英语成绩数据化,并将他们按照“擅长或不擅长的科目相似”进行聚类。
把每个学生都转换成“(语文成绩 , 数学成绩 , 英语成绩)”形式的数据后,就可以将两个数据(c1, m1, e1)和(c2, m2, e2)之间的差距定义为 (c1-c2) + (m1-m2) + (e1-e2) ,其中差距小的数据 就互为“相似的数据”。
符合条件的算法
即使定义好了数据间的差距,聚类的方法也会有很多种。我们可以设定各种各样的条件, 比如想把数据分为 10 个簇,或者想把 1 个簇内的数据定在 30~50 人之间,再或者想把簇内数据 间的最大距离设为 10,等等。而设定什么样的条件取决于进行聚类的目的。
k-means 算法
k-means 算法是聚类算法中的一种,它可以根据事先给定的簇的数量进行聚类。
k-means算法步骤
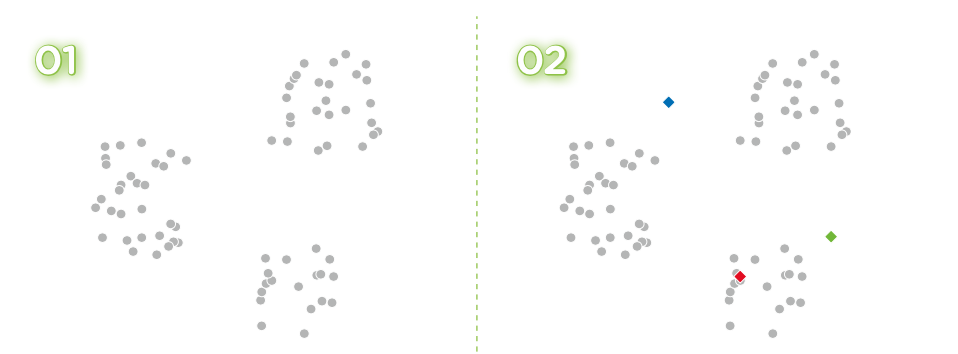
- 首先准备好需要聚类的数据,然后决定簇的数量(比如下面图示簇的数量为3)。
- 随机选择 3 个点作为簇的中心点。
- 计算各个数据分别和 3 个中心点中的哪一个点距离最近。
- 将数据分到相应的簇中。这样,3 个簇的聚类就完成了。
- 计算各个簇中数据的重心,然后将簇的中心点移动到这个位置。
- 重新计算距离最近的簇的中心点,并将数据分到相应的簇中。
- 重复执行“将数据分到相应的簇中”和“将中心点移到重心的位置”这两个操作,直到中心点不 再发生变化为止。
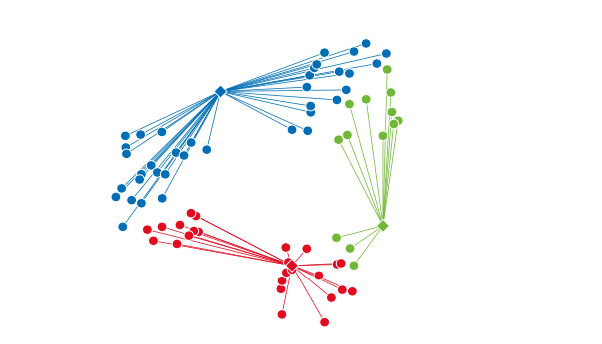
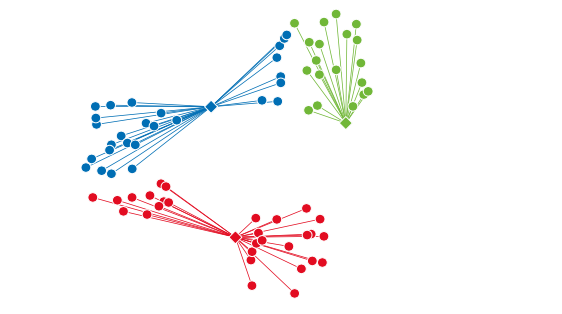
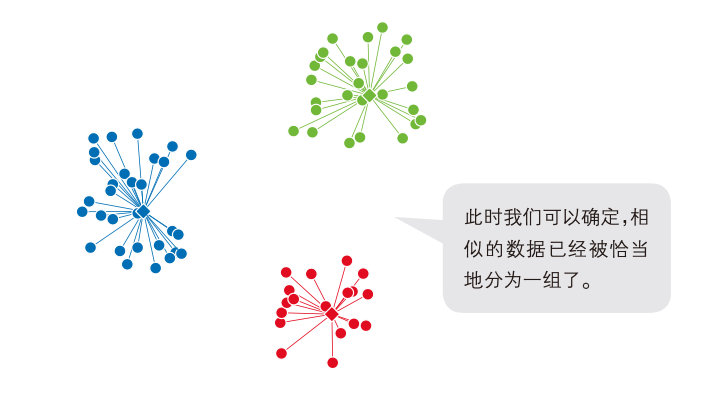
解说:
k-means 算法中,随着操作的不断重复,中心点的位置必定会在某处收敛,这一点 已经在数学层面上得到证明。
前面的例子中我们将簇的数量定为 3,若现在使用同样的数据,将簇的数量定为 2, 那么聚类将如下图所示。
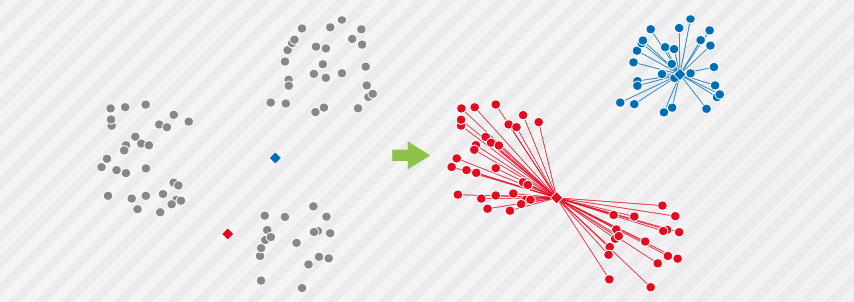
位于左边和下边的两个数据块被分到了一个簇中。就像这样,由于 k-means 算法需 要事先确定好簇的数量,所以设定的数量如果不合理,运行的结果就可能会不符合我们的需求。
如果对簇的数量没有明确要求,那么我们可以事先对数据进行分析,推算出一个合适的数量,或者不断改变簇的数量来试验 k-means 算法。
另外,如果簇的数量同样为 2,但中心点最初的位置不同,那么也可能会出现下图 这样的聚类结果。
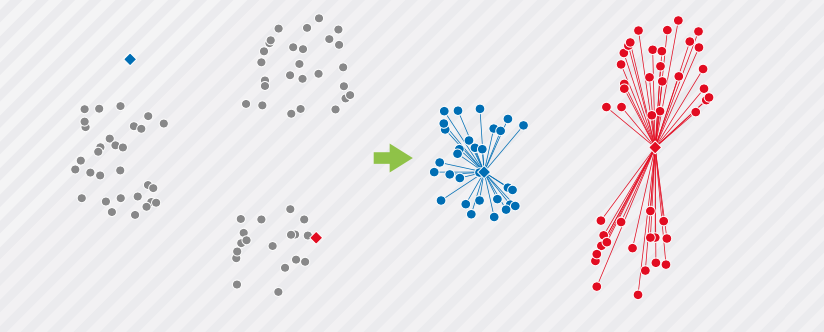
与之前的情况不同,这次右上和右下的两个数据块被分到了一个簇中。也就是说, 即使簇的数量相同,只要随机设置的中心点最初的位置不同,聚类的结果也会产生变化。 因此,我们可以通过改变随机设定的中心点位置来不断尝试 k-means 算法,再从中选择 最合适的聚类结果。
补充说明
除了 k-means 算法以外,聚类算法还有很多,其中“层次聚类算法”较为有名。与 k-means 算法不同,层次聚类算法不需要事先设定簇的数量。
在层次聚类算法中,一开始每个数据都自成一类。也就是说,有 n 个数据就会形成 n 个簇。然后重复执行“将距离最近的两个簇合并为一个”的操作 n-1 次。每执行 1 次, 簇就会减少 1 个。执行 n - 1 次后,所有数据就都被分到了一个簇中。在这个过程中,每个阶段的簇的数量都不同,对应的聚类结果也不同。只要选择其中最为合理的 1 个结果 就好。
合并簇的时候,为了找出“距离最近的两个簇”,需要先对簇之间的距离进行定义。 根据定义方法不同,会有“最短距离法”“最长距离法”“中间距离法”等多种算法。
第七章 其他算法
欧几里得算法
欧几里得算法(又称辗转相除法)用于计算两个数的最大公约数**(GCD:greatest common divisor)**,被称为世界上最古老的算法。
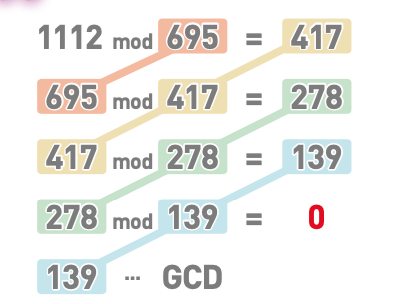
使用欧几里得算法求1112和695的最大公约数
- 首先用较小的数字去除较大的数字,求出余数。也就是对两个数字进行 mod 运算,除完后的余数为417。
- mod运算即取余运算,A mod B 就是算出A除以B后的余数C。
- 接下来再用除数695和余数417进行mod运 算。结果为 278。
- 继续重复同样的操作,对 417 和 278 进行 mod 运算,结果为139。
- 对 278 和 139 进行 mod 运算,结果为 0。也就 是说,278 可以被 139 整除。
- 余数为 0 时,最后一次运算中的除数 139 就是 1112 和 695 的最大公约数。
Java实现
素性测试
素性测试是判断一个自然数是否为素数的测试。素数(prime number)就是只能被 1 和其自身整除,且大于 1 的自然数。
素数从小到大有 2、3、5、7、11、13…目前在加密技术中被广泛应用的 RSA 算法就会用到大素数,因此“素性测试”在该算法中起到了重要的作用。